Young Statisticians talk – May 2019
Each year the WA Branch offers a scholarship worth $1,000 to a Young Statistician completing honours in that year at a Western Australian University. This year’s 2019 winner was Emily Whitney from Curtin University. The prize comes along with a request to deliver next year’s May address to the WA Branch.
 President of the WA Branch, Dr Brenton Clarke, delivers a $1,000 “digital handshake” to Emily Whitney, this year’s winner of the WA Branch Honours Scholarship.
President of the WA Branch, Dr Brenton Clarke, delivers a $1,000 “digital handshake” to Emily Whitney, this year’s winner of the WA Branch Honours Scholarship.
The May meeting of the Western Australia Branch also heard talks from two young statisticians, Michael Dymock and Connor Duffin, both PhD students from the University of Western Australia. Michael talked about his current research with Group Based Trajectory Modelling with Monotonicity Constraints, which aims to better quantify the uncertainty in three-dimensional geological interpolation models and geophysical models through Bayesian inversion. Connor talked about his research on Modelling site-specific Australian daily rainfall with Bayesian mixture models which aims to model monthly rainfall across four different areas in Australia.
Group Based Trajectory Modelling with Monotonicity Constraints- Talk by Michael Dymock
 Michael started his undergraduate Mathematics and Statistics degree in 2014 at the University of Western Australia, before completing his honours degree in 2018. Along with being awarded first class honours for his research project, Michael received honours scholarships from both the Statistical Society of Australia and the International Biometric Society (Australasian Branch). Through his work Michael has taken first place in both the 2017 Woodside Hackathon and the 2018 Worley Parsons Hackathon, and second place in the 2017 Visagio Hackathon.
Michael started his undergraduate Mathematics and Statistics degree in 2014 at the University of Western Australia, before completing his honours degree in 2018. Along with being awarded first class honours for his research project, Michael received honours scholarships from both the Statistical Society of Australia and the International Biometric Society (Australasian Branch). Through his work Michael has taken first place in both the 2017 Woodside Hackathon and the 2018 Worley Parsons Hackathon, and second place in the 2017 Visagio Hackathon.
The understanding and modelling of developmental trajectories in longitudinal data are of fundamental importance across many areas of research with applications ranging from the health and social sciences to that of marketing. Group based trajectory modelling, an application of finite mixture modelling, is often the first choice in approaching the naturally complex task of modelling these trajectories. The group-based strategy acknowledges the possibility of a heterogeneous population by fitting several groups to the data and subsequently treating each group as a distinct entity or sub-population.
In his talk, Michael explained that existing methodology for group-based trajectory modelling, implemented through the SAS procedure TRAJ, has been developed over the past two decades with the addition of numerous extensions such as the ability to jointly analyse multiple trajectories as well as the handling of missing data. However, there is no methodology currently in place to impose constraints of any kind on the trajectories, in particular, monotonicity constraints. Monotonicity constraints on polynomials play a role in data analysis, when it is known, from the underlying physical theory that the response behaves monotonically. In other words, if we know that the response must progress in the one direction (either increasing or decreasing) over the explanatory variable, it is useful to constrain the model to represent this trend accurately. However, due to a multitude of possible reasons such as data entry error and missing data, in these situations, sometimes unconstrained models fail to capture the monotone behaviour, and thus monotonicity constraints are required.
In his work, Michael implemented a new methodology for fitting group-based trajectory models with monotonicity constraints by using the Expectation Maximisation (EM) algorithm. The structure of the EM algorithm allowed him to separate the optimisation routine into two smaller optimisation sub-routines (one that computes the group membership probabilities and another that maximises the likelihood function). Furthermore, to illustrate the effectiveness of his methodology, he demonstrated the use of his implementation on a real-world example in the statistical programming language R. In his example he aimed to model the developmental trajectories of individuals' lung function, in particular, Forced Expiratory Volume measurements, over a period of approximately forty years. This example is of particular interest to us because we know from underlying theory that the response trajectories will be monotonically decreasing. However, Michael showed that this unconstrained model fails to capture the required monotone behaviour. After re-running the same analysis under monotonicity constraints, Michael was able to show that the implementation is able to effectively capture and model the required monotonic trajectories.


Modelling site-specific Australian daily rainfall with Bayesian mixture models- talk by Connor P. Duffin
Connor completed an Honours degree in Mathematics and Statistics from UWA in 2018, under the supervision of Edward Cripps. Connors research was in the field of Bayesian computational statistics, on modelling Australian daily rainfall. Having stayed in this field, Connor is currently pursuing a PhD at UWA, focussing on quantifying and explaining uncertainties in numerical oceanographic models.
Daily rainfall has a large impact on the social behaviour of human beings, and also has wide agricultural, biological, and economic effects. Being able to model location-specific daily rainfall, across the country, is therefore of utmost importance. There are three principal complexities in modelling daily rainfall at a single location: temporal evolution, zero and missing days, and extreme tail behaviour.
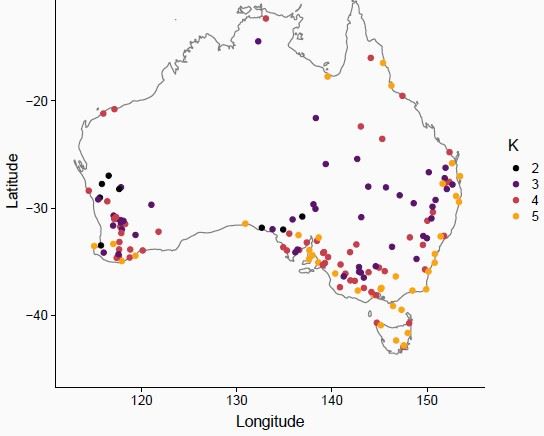
Connors work aims to investigate models that are able to capture these complexities across 151 individual rainfall measurement locations (sites) across Australia. Connor used the finite mixture model as a framework to model the discrete and continuous data that comprise these measurements. There were four main features of the data that Connor had to work around; the seasonality of rainfall, missing data when no measurements were taken, zero-days when there was no rainfall and fat-tails when there are days with intense rainfall. Taking this into account, Connor used the Finite mixture model incorporating temporal evolution model, which captured data with no rainfall and also for days with rainfall. The varying intensities of rainfall were captured through the gamma distribution.
 Some notes:
Some notes:
- 1. Dirac delta to capture zeroes.
- 2. Mixture of gamma PDFs to capture non-zeroes.
- 3. Gamma PDFs analogous to rainfall amounts? Difficult to interpret for K > 3 though.
- 4. Connors approach: Use variation in K = 2, 3, 4, and 5 gamma densities to see how well the model captures tail behaviour.
Temporal evolution is incorporated through the use of a mixture-of-experts structure on the mixture weights. Connor used the Markov chain Monte Carlo to estimate the model.
The results were then analysed through posterior predictive checking, and optimal models where decided on through formal model diagnostics. Connor is eager to continue working on the model and has plans to further investigate if there are other factors that might affect the choice of the model.

After the talks, Michael and Connor where joined by fellow Statisticians for dinner at Tiamos restaurant, where they talked about their future plans and how eager they are to continue to optimise and implement their research on a more broader scale.
Deneegan Subramanian
